3月14日，是国际数学日。这就不得不说说我国古代数学了，尤其是数学中取得的众多算法成就，其中“增乘开方法”更是闪耀着独特的智慧光芒。

增乘开方法，即我国古代数学中求高次方程数值解的方法，由北宋数学家贾宪所创。其核心是通过随乘随加的方式，逐步求出高次方程正根的近似值。该方法蕴含着递归和迭代的数学思想，与现代计算机算法中的迭代法在本质上有相通之处，体现了我国古代数学家对数学算法的深刻理解和卓越创造能力。

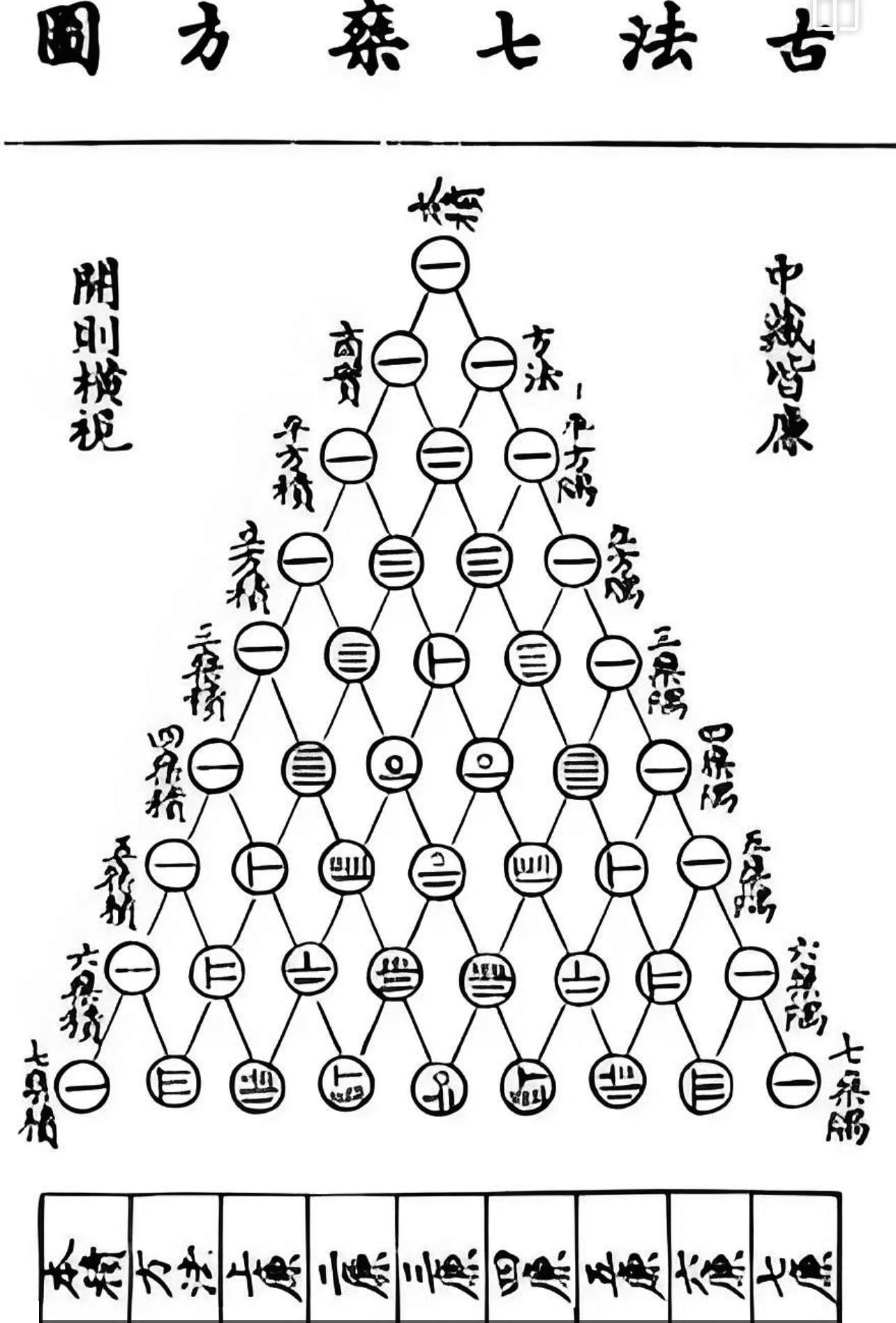
高次方程数值解法始于中算开平方法。南北朝时期称之为开方术，其开方过程称为“开方除之”，至迟在《九章算术》少广章中提出完整的开平方、开立方程序，奠定了中国开方术的基础。我国古典数学在宋元时期达到顶峰，北宋数学家贾宪针对刘徽、《孙子算经》等对《九章算术》开方术的改进，提出了“立成释锁法”和“增乘开方法”，并收录在他于1023年至1034年所著的《黄帝九章算经细草》中。后该书佚失，所幸主要内容被《永乐大典》和杨辉的《详解九章算法》保存下来，才得以传世。《详解九章算法》载有“开方作法本源”图，注明“贾宪用此术”，也就是著名的“贾宪三角”或“杨辉三角”。

贾宪“立成释锁法”中，“立成”是唐宋历算学家将一些常数列成的算表，“释锁”是将开方比喻为打开一把锁，故而，释锁法是借助一个常数表进行开方的方法。该算表便是“开方作法本源”图，相当于整次幂二项式的展开式系数自上而下摆成等腰三角形。此三角的名称也有争议，在《永乐大典》《详解九章算法》等书中，有称五乘、六乘、七乘（即古法七乘方图）的，故均注名贾宪术，统称“贾宪三角”。

“开方作法本源”图下有五句话：“左袤乃积数，右袤乃隅算，中藏者皆廉，以廉乘商方，命实而除之。”前三句说明了其结构，即积、隅、兼、法的位置，后两句概括了各系数在开方计算中的作用。但在实际操作过程中，一般限于被开方数不大或开方次数不高的情况，对于复杂的开方运算实际操作价值有限。为此，贾宪还给出了增乘开方法。他首先给出“增乘方求廉法草”，用这种方法可写出任意层数的贾宪三角。

贾宪将求各廉的随乘随加方法推广到开方术中，创造了增乘开方法。该方法的关键是在得出根的某位得数后，如果需要继续开方，就以商的该位得数自下而上递乘递加，每次低一位而止，以求减根方程。使之更加程序化和机械化，极具创造性和前瞻性。

增乘开方法经过12世纪刘益等人的发展，到南宋秦九韶著《数书九章》（1247年）中提出正负开方术，将求解高次方程正根的方法发展到十分完备的程度。另外，金元数学家李冶、朱世杰等人也补充了该算法，为13世纪的天元术及14世纪的四元术方程求解提供了条件。

用增乘开方法开平方和开立方要比传统开方法简便，并且可以推广到求任何高次幂开方问题。它的诞生标志着开方学术发展到了一个新阶段。

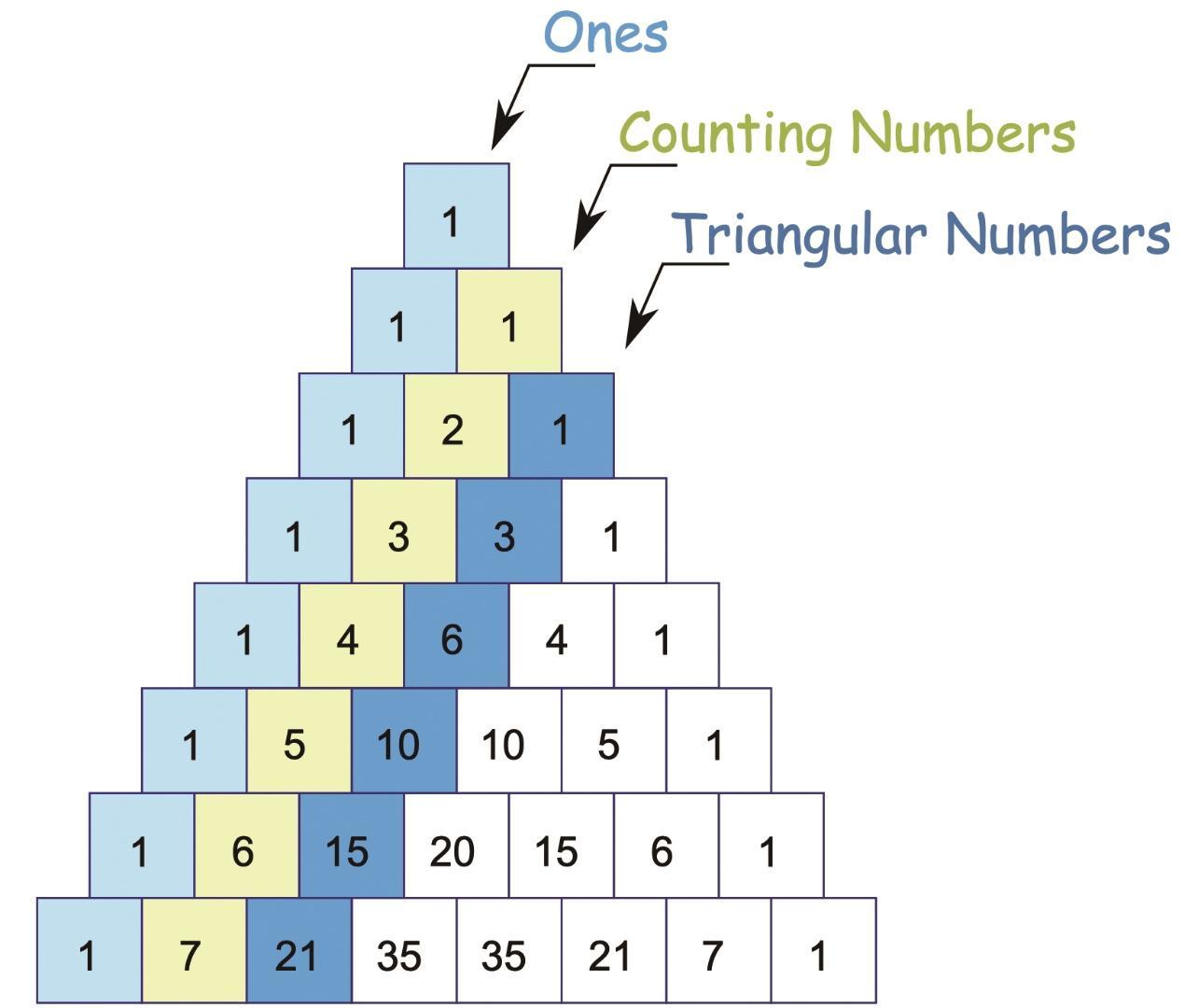
1654年，法国数学家布莱士·帕斯卡在《算术三角形》中系统研究了二项式系数的性质，并命名“算术三角”，后被广泛称为“帕斯卡三角”，但它却比贾宪三角晚了600多年。当然，帕斯卡的研究更注重三角的抽象数学性质（如组合数、递推关系），这与贾宪的应用导向不同。

由于西方学界长期忽视非欧洲数学贡献，帕斯卡因系统性研究被广泛命名，而贾宪的成就直到20世纪才被国际数学界重新发现。

贾宪三角是我国古代数学领先世界的例证，而帕斯卡三角因融入近代数学体系影响更为广泛。

现代数学界通常以“二项式系数三角”统称这一结构，我们是认可的。但若论起源，贾宪的贡献应被明确承认。

（作者系国家教育咨询委员会委员、中国科技馆原馆长）